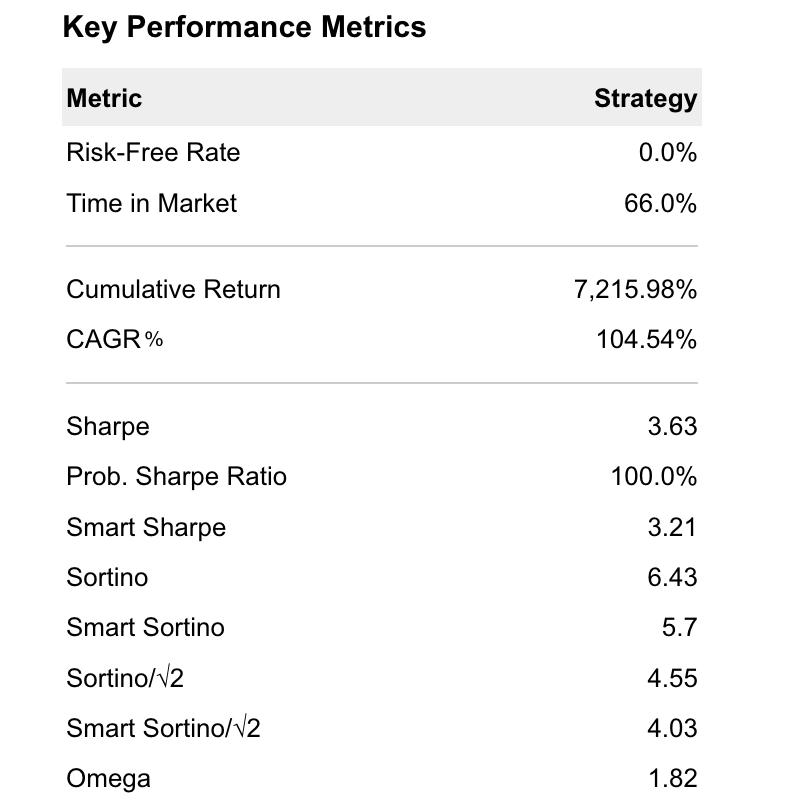
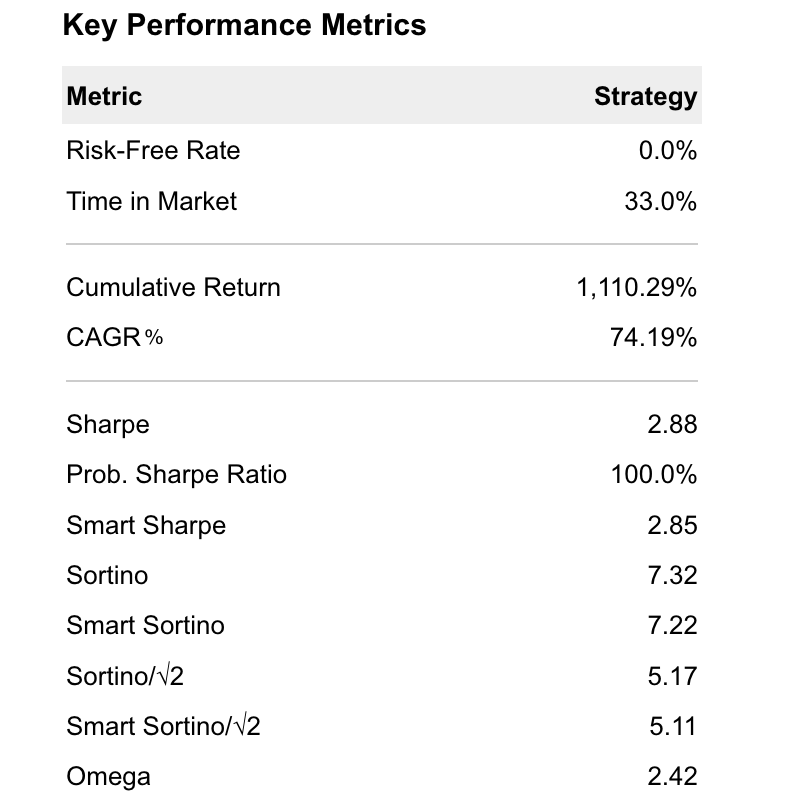
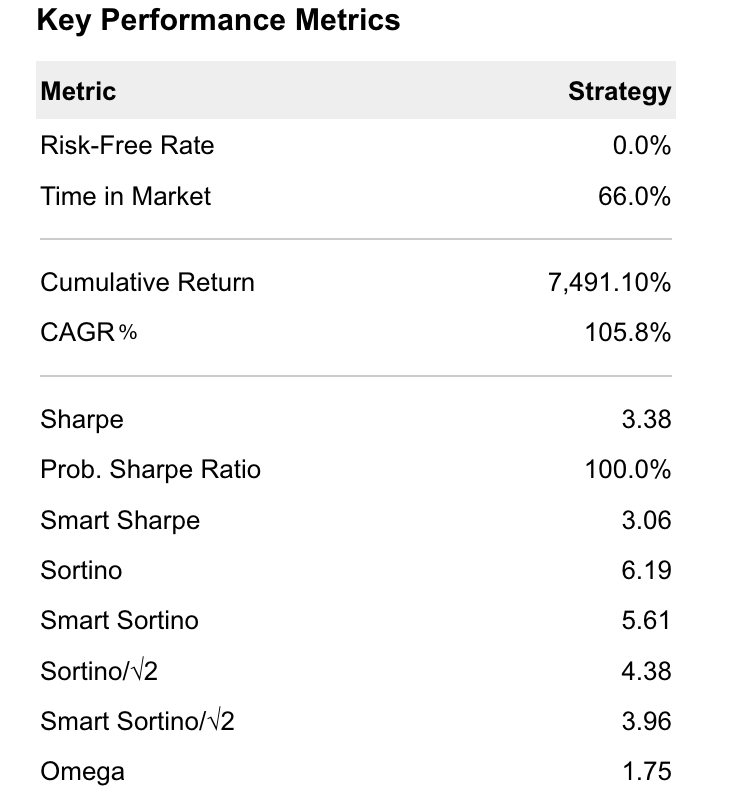
Expanded Introduction

Algorithmic trading is no longer the exclusive domain of hedge funds and investment banks. With increasing access to computational power and real-time data, quantitative strategies are now applied across asset classes and by a wide range of participants—from institutional investors to crypto-native trading desks. Among the countless approaches to trading, two stand out as fundamental building blocks: momentum and mean reversion.

Both approaches have deep historical roots. Momentum strategies can be traced back to the early 20th century, when traders like Richard Wyckoff emphasized trend-following. Mean reversion, on the other hand, connects to even older theories such as the “Law of Averages” in probability and Bachelier’s 1900 thesis on Brownian motion in markets.

While they may seem mutually exclusive, momentum and mean reversion actually complement each other. By exploring their mathematical foundations, empirical evidence, and practical implementation, we can understand why combining them leads to more robust algorithmic portfolios.

Momentum in Depth

Mathematical Representation

Momentum is often defined as the rate of change in price. A simple formula for momentum over period n is:

For portfolio-level strategies, momentum can also be measured by ranking assets based on their past performance and selecting the strongest and weakest performers (cross-sectional momentum).

Empirical Evidence

• Jegadeesh & Titman (1993): Showed that U.S. stocks with high returns over the past 3–12 months continued to outperform in the following months.
• Fama & French (1996): Acknowledged momentum as one of the “anomalies” unexplained by the efficient market hypothesis.
• Asness, Moskowitz, and Pedersen (2013): Demonstrated that momentum exists across global equities, bonds, commodities, and currencies.

These studies show that momentum is not an isolated phenomenon but a pervasive market characteristic.

Real-World Case Study

During the Dot-com Bubble (1998–2000), momentum strategies thrived by riding the parabolic growth of tech stocks. Traders using moving average filters and breakout systems captured significant returns. However, when the bubble burst, many pure-momentum traders faced devastating losses—illustrating the importance of diversification.

Mean Reversion in Depth

Mathematical Representation

Mean reversion assumes that prices oscillate around a statistical mean. One of the most common tools is the Z-score, which measures how many standard deviations the price deviates from its mean:

Empirical Evidence

• Lo and MacKinlay (1990): Provided evidence that stock returns are not purely random but exhibit mean-reverting properties.
• Poterba & Summers (1988): Found that stock prices show mean-reversion tendencies over long horizons (3–5 years).
• Crypto Markets: Studies of Bitcoin (Urquhart, 2016) found both momentum and mean reversion phases, with early markets exhibiting stronger inefficiencies.

Real-World Case Study

The 2010 Flash Crash provided a textbook example of mean reversion. Within minutes, the Dow Jones Industrial Average plunged nearly 1,000 points before recovering most of the losses the same day. Mean reversion algorithms exploiting extreme deviations captured significant intraday profits.

Why Combining Momentum and Mean Reversion Works

Market Regime Dependence

Markets alternate between trending phases and range-bound phases. Relying solely on momentum or mean reversion exposes traders to regime risk. By combining the two, portfolios adapt dynamically to changing conditions.

Portfolio Diversification

Empirical backtests show that blending momentum and mean reversion lowers volatility and reduces drawdowns. For instance, a portfolio of S&P 500 stocks combining 12-month momentum with short-term mean reversion generated more consistent Sharpe ratios than either strategy alone.

Institutional Case Study

AQR Capital Management, one of the largest quant funds globally, integrates momentum as a core factor but hedges it with mean reversion and value-based strategies. This balanced approach has allowed AQR to maintain long-term profitability despite cyclical underperformance in single factors.

Advanced Enhancements

Volatility Clustering

Volatility clustering, observed by Mandelbrot and later formalized in GARCH models, highlights that markets experience periods of high volatility followed by calm phases. Algorithms using volatility regimes can decide when to emphasize momentum (high-volatility trends) versus mean reversion (low-volatility ranges).

Machine Learning Integration

Machine learning models enhance regime detection by classifying markets into trending, mean-reverting, or neutral states. Reinforcement learning agents can even allocate dynamically between strategies, improving adaptability.

Risk Management Layer

No strategy succeeds without risk controls. Combining momentum and mean reversion requires strict oversight:

• Position sizing based on volatility.
• Correlation checks to avoid redundant exposure.
• Dynamic capital allocation across strategies.

Extended Case Studies

Global Commodities Supercycle (2003–2008)

Between 2003 and 2008, commodities such as oil, copper, and agricultural products experienced one of the strongest rallies in history, driven largely by China’s industrial expansion and global demand growth. Momentum strategies thrived by capturing multi-year uptrends, while mean reversion traders repeatedly shorted perceived “overbought” conditions and were punished as prices kept climbing. The lesson: during structural shifts, momentum dominates and ignoring it can be fatal.

Crypto Bear Market (2018)

After Bitcoin peaked near $20,000 in late 2017, the crypto market entered a brutal bear phase throughout 2018. Momentum traders who continued applying breakout systems suffered large losses as the trend remained persistently negative. In contrast, mean reversion systems profited from short-lived bounces and sideways consolidations. This case illustrates that even in long bear markets, different strategies can extract profits if properly aligned with market conditions.

COVID-19 Pandemic Shock (2020)

In March 2020, global equity markets collapsed by more than 30% within weeks, driven by the uncertainty of the COVID-19 outbreak. Momentum systems captured the sharp downside moves by riding the collapse, while mean reversion systems entered opportunistic trades during oversold conditions, benefiting from the rapid rebound supported by central bank interventions. This dual-strategy setup was among the best performers of the decade.

The Swiss Franc Shock (2015)

On January 15, 2015, the Swiss National Bank unexpectedly abandoned its currency peg to the euro. Within minutes, the Swiss franc appreciated by nearly 30%, sending shockwaves across global markets. Momentum traders who quickly recognized the trend captured massive profits, while mean reversion systems suffered heavily as they tried to fade the move, expecting a reversal that never came. The event highlighted the importance of regime detection in real-time.

The “Meme Stock” Mania (2021)

In early 2021, stocks such as GameStop (GME) and AMC surged thousands of percent due to coordinated retail buying pressure fueled by social media platforms like Reddit. Momentum systems captured the explosive rallies, while mean reversion strategies initially struggled. However, once the hype subsided, mean reversion traders found opportunities in the subsequent crashes and stabilization. The takeaway: both strategies can work, but timing is everything.

Conclusion

Momentum and mean reversion are not mutually exclusive philosophies but complementary tools in the algorithmic trader’s arsenal. Academic research and decades of market evidence confirm their effectiveness across asset classes and timeframes. Traders who embrace both approaches—through regime detection, multi-strategy portfolios, and advanced risk management—are better positioned to achieve consistent, long-term success.

In a world of increasing volatility and rapid structural changes, adaptability is the ultimate edge. And that adaptability is best achieved by balancing the twin pillars of modern algorithmic trading: momentum and mean reversion.